11 major reasons for simulating electronic design and causing noise

Noise is a core issue in analog circuit design, which directly affects the amount of information that can be extracted from measurements and the economic cost of obtaining the information you need. Unfortunately, there is a lot of confusion and misleading information about noise that can lead to poor performance, high cost over-engineering, or inefficient use of resources.

This article describes 11 long-standing misunderstandings about noise analysis in analog designs.

1. Reducing the resistance value in the circuit always improves the noise performance.

The noise voltage increases with increasing resistance. The relationship between the two is well known and can be described by the Johnson noise equation: erms = √4kTRB, where erms is the rms voltage noise and k is the Boltzmann constant. T is the temperature (in K), R is the resistance value, and B is the bandwidth. This led many engineers to conclude that in order to reduce noise, the resistance should be reduced. Although this is often true, it should not be considered universal in this regard, because in some cases, larger resistances can improve noise performance. For example, in most cases, the method of measuring current is to pass it through a resistor and then measure the resulting voltage. According to Ohm's law V = I × R, the generated voltage is proportional to the resistance value, but as shown in the above equation, the Johnson noise of the resistor is proportional to the square root of the resistance value. Due to this relationship, the signal-to-noise ratio can be increased by 3 dB for every doubling of the resistance value. This trend has been correct until the resulting voltage is too high or the power consumption is too high.

2. The noise spectral density of all noise sources can be added together, and the bandwidth can be considered in the final calculation.

Adding the noise spectral density (nV/√Hz) of multiple noise sources (the voltage noise source is rooted by the square root) without calculating the rms noise of each noise source separately, saving time, but this simplification is only applicable. The same bandwidth seen by each noise source. If the noise sources see different bandwidths, simply adding them becomes a terrible trap. Figure 1 shows the situation in an oversampling system. From the noise spectral density, the total noise of the system seems to be dominated by the gain amplifier, but once the bandwidth is considered, the rms noise contributed by each level is actually very similar.

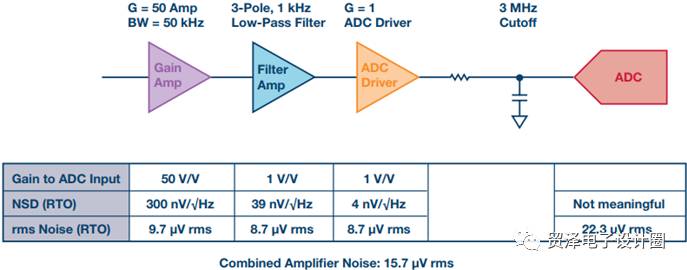Figure 1. Reasons for noise calculation using rms noise instead of spectral density

3. Every noise source must be included in the manual calculation

Some people may not be able to consider every source of noise during design, but the time of the design engineer is precious, which can be very time consuming in large designs. Comprehensive noise calculations are best left to the simulation software. But how do designers simplify the manual noise calculations needed for the design process? The answer is to ignore unimportant noise sources below a certain threshold. If a noise source is the 1/5 erms value of the main noise source (or any other noise source that is converted to the same point), its contribution to the total noise will be less than 2%, which can reasonably be ignored. Designers often argue that where the threshold should be chosen, but whether it is 1/3, 1/5, or 1/10 (to increase total noise by 5%, 2%, and 0.5%, respectively), the design is sufficient for full simulation or Before the degree of calculation, there is no need to worry about smaller noise sources below this threshold.

4. Should choose an ADC driver with noise of ADC 1/10

Analog-to-Digital Converter (ADC) data sheets may suggest using a low-noise ADC driver amplifier with noise around 1/10 of the ADC to drive the analog input. However, this is not always the best option. In a system, it is often worthwhile to weigh the ADC driver noise from a system perspective.

First, if the noise source before the ADC driver in the system is much larger than the ADC driver noise, then choosing an ultra-low noise ADC driver will not bring any benefit to the system. In other words, the ADC driver should be commensurate with the rest of the system.

Second, even in the simple case of only one ADC and one driver amplifier, it is still advantageous to weigh the noise and determine its impact on the system. The reasons for this can be more clearly understood by specific values. Consider a system with a 16-bit ADC with an SNR value equivalent to 100 μV rms noise, and an amplifier used as an ADC driver with 10 μV rms noise. Adding these noise sources by sum and root gives a total noise of 100.5 μVrms, which is very close to the noise of the ADC alone. Consider the following two solutions that make the amplifier and ADC more balanced and their impact on system performance. If a similar 18-bit ADC is used instead of a 16-bit ADC, the former's rated SNR is equivalent to 40 μV rms noise, and the total noise becomes 41 μV rms. Alternatively, if a 16-bit ADC is reserved, but a lower power amplifier is used instead of the above driver, which contributes 30 μV rms of noise, the total noise becomes 104 μV rms. In terms of system performance, one of the above two options may be a better choice than the original combination. The key is to weigh the pros and cons and its impact on the system as a whole.

5. 1/f noise must always be considered in DC-coupled circuits

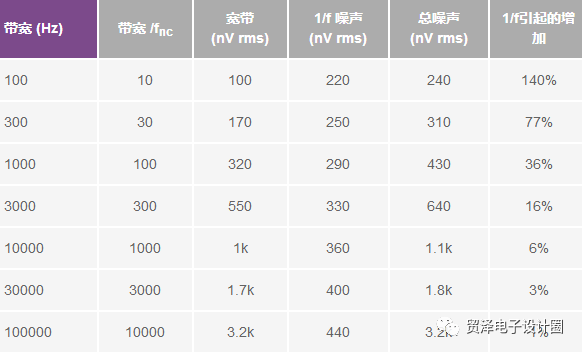
1/f noise is a major threat to ultra-low frequency circuits because many common noise suppression techniques, such as low-pass filtering, averaging, and long-term integration, are ineffective. However, the noise of many DC circuits is dominated by white noise sources, and 1/f noise does not contribute to the total noise, so there is no need to calculate 1/f noise. To clarify this effect, consider an amplifier with a 1/f noise corner frequency fnc of 10 Hz and a broadband noise of 10 nV/√Hz. For various bandwidths, the circuit noise with and without 1/f noise in the 10 second acquisition time is calculated to determine the effect of 1/f noise. When the bandwidth is 100 times that of fnc, broadband noise begins to dominate; when the bandwidth exceeds 1000 times of fnc, 1/f noise is negligible. Modern bipolar amplifiers can have much lower noise corner frequencies than 10 Hz, and zero-drift amplifiers almost completely eliminate 1/f noise.

Table 1. Example of relationship between 1/f noise effect and circuit bandwidth

6. Since the 1/f noise increases as the frequency decreases, the DC circuit has infinite noise.

Although DC is a useful concept for circuit analysis, the real situation is that if DC is considered to be operating at 0 Hz, then there is actually no such thing. As the frequency gets lower and lower, approaching 0 Hz, the cycle will become longer and longer, approaching infinity. This means that there is a minimum frequency that can be observed, even if the circuit is theoretically a DC response. The minimum frequency depends on the acquisition duration or aperture time, which is the length of time the observed device is output. If an engineer turns on the device and observes the output for 100 seconds, the lowest frequency artifact it can observe is 0.01 Hz. This also means that the lowest frequency noise that can be observed at this time is also 0.01 Hz.

Now expand the description with a numerical example, consider a DC to 1 kHz circuit and continuously monitor its output. If a certain amount of 1/f noise in the circuit is observed in the first 100 seconds, from 0.01 Hz to 1 kHz (5 octave frequencies), then in 30 years (about 1nHz, 12 ten octaves) The amount of noise observed can be calculated as √12/5 = 1.55, or 55% more than the noise observed in the first 100 seconds. This increase has little meaning, even if the worst case is considered - 1/f noise continues to increase to 1 nHz (there is currently no measurement evidence) - as is the case. In theory, if the aperture time is not clearly defined, the 1/f noise can be calculated to a frequency equal to the reciprocal of the circuit lifetime. In practice, the deviation of the circuit over such a long period of time is dominated by aging effects and long-term drift, rather than 1/f noise. Many engineers set the lowest frequency, such as 0.01 Hz or 1 mHz, for the noise calculation of the DC circuit to make the calculations realistic.

7. Noise equivalent bandwidth will double the noise

The noise equivalent bandwidth (NEB) is a useful simplification for noise calculation. Since the gain above the cutoff frequency is not zero, some noise that exceeds the circuit bandwidth will enter the circuit. NEB is the calculated cutoff frequency of the ideal brick wall filter, which puts the same amount of noise as the actual circuit. NEB is larger than –3 dB bandwidth and has been calculated for common filter types and orders. For example, for a single-pole low-pass filter, it is 1.57 times the –3dB bandwidth and is written in the formula NEB1-pole = 1.57 × BW3dB. However, there seems to be confusion about where the multiplication factor should be placed in the noise equation. Keep in mind that NEB regulates bandwidth, not noise, so it should be under the root number as shown below:

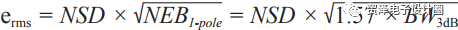
8. The lowest voltage noise amplifier is the best choice

When op amps are selected, voltage noise is often the only noise specification that designers consider. In fact, current noise can not be ignored. Unless special circumstances such as input bias current compensation, the current noise is usually the shot noise of the input bias current: in = √2 × q × IB. Current noise is converted to voltage by source resistance, so if there is a large resistance in front of the amplifier input, current noise may contribute more to system noise than voltage noise. A typical case where current noise can be a problem is when a low noise operational amplifier is used and its input is connected in series with a large resistor. For example, consider the low noise op amp ADA4898-11 with a 10 kΩ resistor in series with its input. The voltage noise of the ADA4898-1 is 0.9 nV/√Hz, the noise of the 10 kΩ resistor is 12.8 nV/√Hz, and the current noise of 2.4 pA/√Hz is multiplied by 10 kΩ. The resistance is equal to 24nV/√Hz. This is the largest noise source in the system. . In situations where current noise dominates, devices with lower current noise are often found to reduce system noise; especially for precision amplifiers, but high-speed FET input operational amplifiers may also be useful for high-speed circuits. For example, if you do not select the ADA4898-1 (and thus do not get the benefit of voltage noise as low as 0.9 nV/√Hz), you can choose a JFET input amplifier such as the AD8033 or ADA4817-1.

9. Provide most of the gain in the first stage for optimal noise performance

In order to achieve better noise performance, it is often recommended to provide gain in the first stage, which is true because the signal will be larger than the noise of subsequent stages. However, the disadvantage of doing so is that it can weaken the maximum signal that the system can support. In some cases, rather than providing a large portion of the gain in the first stage (although this increases the sensitivity of the measurement, but limits the dynamic range), it is better to limit the gain provided by the first stage and digitize it with high resolution to make the sensitivity and The dynamic range is maximized.

10. When the resistance is given, the noise of all types of resistors is the same

The Johnson noise of the resistor is so important that we need a simple formula to calculate the noise of a resistor at a certain temperature. However, Johnson noise is the smallest noise that can be observed in a resistor, and not all types of resistors have the same noise. There is also excessive noise, which is one of the sources of 1/f noise in the resistor and is closely related to the type of resistor. Excessive noise (sometimes also referred to as current noise) is related to the way the current flows in a discontinuous medium. It is specified as the noise figure (NI) in dB, based on 1 μV rms/Vdc per decade. This means that if there is 1 Vdc on a 0 dB NI resistor, the excess noise at 10 octaves is 1 μV rms. The highest NI for carbon and thick film resistors can be as high as +10 dB, which is best avoided in the noise-sensitive portion of the signal path. The sheet resistance is generally much better, about –20 dB; the foil and wirewound resistance can be less than –40 dB.

11. Given a sufficiently long acquisition time, the averaging method can reduce the noise to infinitesimal

It is generally believed that the mean method reduces the noise by a square root of the mean. This is true under certain conditions, ie the NSD must remain flat. However, in the 1/f range and in several other cases, this relationship does not hold. Consider using the averaging method in a system that samples at a constant frequency fs, averaging n samples and performing 1/n extraction, and returning m samples. Taking n average values ​​will change the effective sampling rate after fetching to fs/n, the effective maximum frequency seen by the system is reduced by n times, and the white noise is reduced by √n times. However, the time to get m samples is also extended by a factor of n, so the lowest frequency that the system can see is also reduced by n times (remember, there is no such thing as 0 Hz). The more the average number is taken, the lower the maximum and minimum frequencies in the band are. Once the maximum and minimum frequencies are in the 1/f range, the total noise depends only on the ratio of these frequencies, and increasing the mean number has no further benefit in reducing noise. The same applies to the long integration time of an integrated ADC with multiple slopes. In addition to the mathematical limitations, there are other practical limitations. For example, if quantization noise is the dominant source of noise such that the ADC output at the DC input voltage is a flicker-free constant code, any number of averages will return the same code.

Reference circuit

Motchenbacher, CD and JA Connelly. Low noise electronic system design. Wiley, 1993.

Author

Scott Hunt is a systems applications engineer in the Linear and Precision Technology Division of ADI (Wilmington, MA), specializing in precision instrumentation. In 2011, Scott joined Analog Devices as a Product Applications Engineer and was responsible for high-performance integrated precision amplifiers such as instrumentation amplifiers. He holds a bachelor's degree in electrical and computer systems engineering from Rensselaer Polytechnic Institute. Scott received the ADI's 2015 Outstanding Technical Writing Award and the 2015 Outstanding Program Support Award.