Logistic regression, also known as logistic regression analysis, is a generalized linear regression analysis model. It is often used in fields such as data mining, automatic disease diagnosis, and economic forecasting.
Logistic regression is a linear regression that starts with a continuous value whose output is actually meaningful, and thus has many similarities to the multiple linear regression analysis.
Logistic regression model
Logistic regression is an easily understandable model that is equivalent to y=f(x), indicating the relationship between the independent variable x and the dependent variable y. The most common problems are: When a doctor treats a patient, he or she decides whether or not the patient is ill or has a disease. One of the questions is to obtain the independent variable x, that is, the characteristic data. Judging whether or not you are sick is equivalent to obtaining the dependent variable y, and predicting classification.
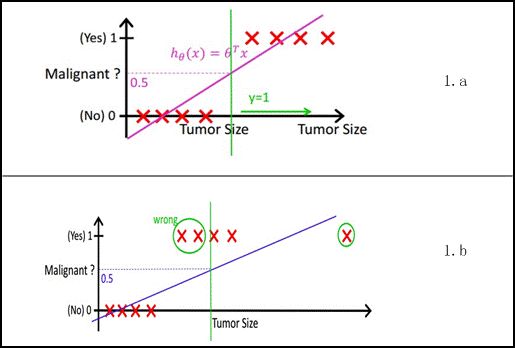
Figure 1 Linear regression example
The simplest regression is a linear regression. Using Andrew NG's handouts, as shown in Figure 1.a, x is the data point --- the size of the tumor, y is the observation value --- if there is a malignant tumor. By constructing a linear regression model, as shown in hθ(x), after constructing a linear regression model, it can be predicted whether or not it is malignant according to the size of the tumor. hθ(x) ≥ 0.5 is malignant, and hθ(x) < 0.5 is benign.
At the same time, the robustness of linear regression is very poor. For example, in the data set of Fig. 1.b, regression is established. Because of the presence of the rightmost noise, the regression model performs poorly on the training set. This is mainly due to the linear sensitivity of the linear regression in the entire real number domain, and the scope of the classification needs to be in [0,1]. Logistic regression is a regression model that reduces the prediction range and limits the prediction value to [0,1]. The regression equation and regression curve are shown in Figure 2. The logic curve is very sensitive at z=0 and is not sensitive at z>>0 or z<<0, limiting the prediction to (0,1).
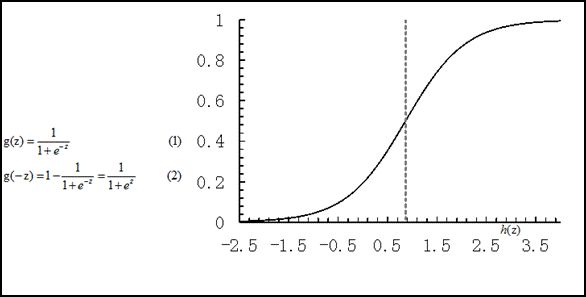
Figure 2 Logical equations and logic curves
Logical regression is only based on linear regression, applying a logical function, but also because of this logical function, logical regression has become a bright star in the field of machine learning, but also the core of computational advertising, for multiple logic Regression can be approximated and classified by the following formula. Among them, the transformation of formula (4) will bring many benefits to the simplified formula when the parameters of the logistic regression model are estimated. y={0,1} is the classification result.
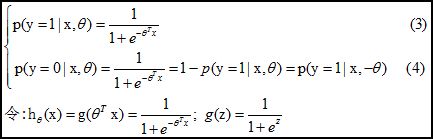
2. Decision boundary
Why does logistic regression solve the classification problem? We can use the boundary of the interpretation to explain, it can be understood as the boundaries of the data divided by different categories, the sides of the boundary should be different types of data.
From the two-dimensional rectangular coordinate system, to give a few examples, it is probably the following three types:
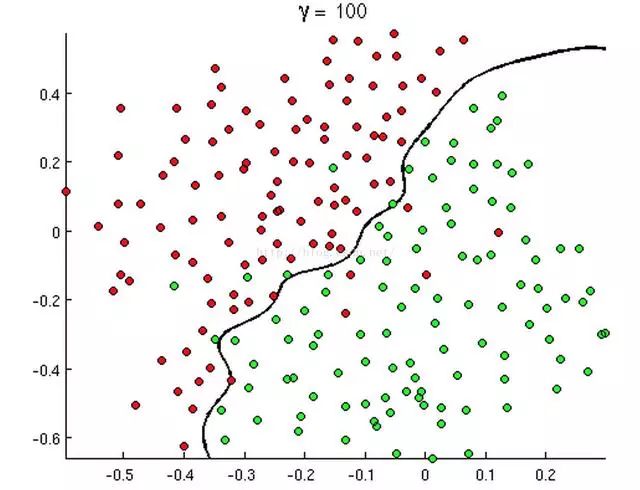
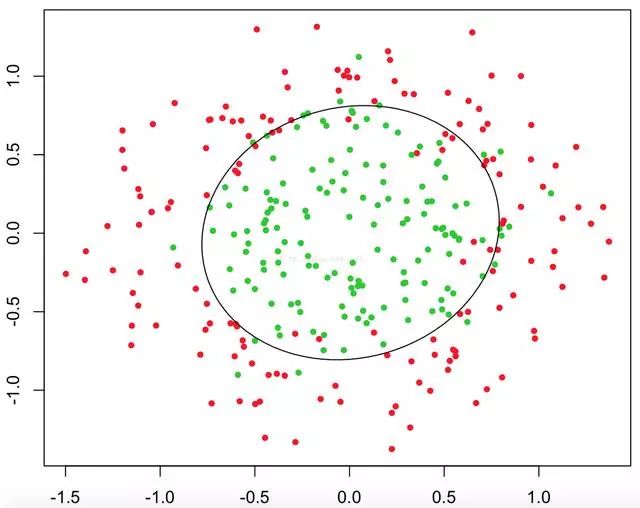

From the above three images, the red and green sample points are different types of samples, and the lines we draw, whether straight lines, circles or curves, can better separate the two types of samples in the figure. This is what we call the decision boundary. Then how does the logistic regression obtain these decision boundaries based on sample points?
We still borrow some examples from Professor Andrew NG's course to explain this issue.
Returning to the sigmoid function, we find that when g(z)≥0.5, z≥0; for hθ(x)=g(θTX)≥0.5, then θTX≥0, this means that the estimated y=1; When predicting y = 0, θTX<0; so we think that θTX=0 is a decision boundary. When it is greater than 0 or less than 0, the logistic regression model predicts different classification results. Let us look at the first example hθ(x)=g(θ0+θ1X1+θ2X2), where θ0, θ1, and θ2 take -3, 1, 1 respectively. Then, when −3+X1+X2≥0, y=1; then X1+X2=3 is a decision boundary. The graph is as follows, which is just to distinguish the two types of points on the graph:

Example 1 is just a linear decision boundary. When hθ(x) is more complex, we can obtain nonlinear decision boundaries. For example:
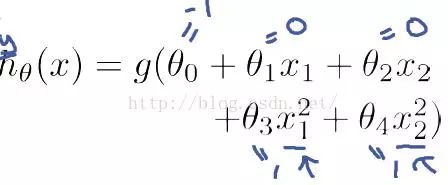
At this time, when x12 + x22 ≥ 1, we determine y = 1, the decision boundary at this time is a circle, as shown in the following figure:
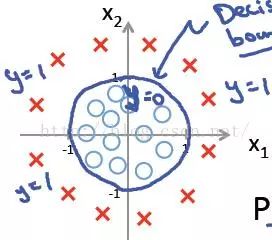
Therefore, we find that theoretically, as long as our hθ(x) design is reasonable enough to accurately say that θTx in g(θTx) is sufficiently complex, we can fit different decision boundaries in different situations, and thus Different sample points are separated.
Intuitive understanding of logistic regression in two-dimensional space is a feature of the singmoid function that allows the decision threshold to map to a decision boundary of the plane. Of course, as the complexity of the feature, the decision boundary may be a variety of features, but it Can better separate the two types of sample points to solve the classification problem.
Disposable vape pen Onlyrelx 500puffs is portable and fashion disposable electronic cigarette, disposable ecigs pen are trending featured vape pen for vapors as it's safety and easy to use. Disposable vape pod,disposable vape, wholesale vape,vape wholesale,vape pen manufacturer and supplier.disposable vape pen,disposable electronic cigarette,disposable ecigs pen,disposable ecigs stick,disposable e-cigs pen,disposable vape factory,disposable vape pod,disposable vape device,vape pen,vape stick, vape wholesale,wholesale vape,customized dispsoable vape pen,customized vape pen,OEM&ODM disposable ecigs pen,disposable electronic cigarette wholesale, wholesale disposable electronic cigarette,distribute vape pen,vape pen distribute,high quality vape pen,high quality vape pod,rechargeable disposable vape pen,refillable vape pen,refilling electronic cigarette,rechargeable disposable electronic cigarette,refillable vape pod,disposable refillable ecigs,disposable refilling e-cigs pen,refillable e-cigs pen
Onlyrelx mini500,Onlyrelx vape bar,Mini Vaporizer Onlyrelx,Original Onlyrelx Vape Pen,disposable vape pen
Shenzhen Onlyrelx Technology Co.,Ltd , https://www.onlyrelxtech.com