The use of capacitive decoupling is the main method to solve the problem of power supply noise. This method is very effective for improving the response speed of transient current and reducing the impedance of the power distribution system.
For capacitive decoupling, many materials are involved, but the angle of explanation is different. Some are explained from the perspective of local charge storage (that is, energy storage), some are explained from the perspective of impedance of the power distribution system, and some materials are more confusing. Many people feel a little confused when looking at the information. In fact, these two formulations are essentially the same, but the perspective of looking at the problem is different.
1. Explain the principle of capacitive decoupling from the perspective of energy storage.
When making a circuit board, many capacitors are usually placed around the load chip, and these capacitors act as power decoupling. The principle can be illustrated in Figure 1.
(Formula 1)
As long as the capacitance C is large enough, with only a small voltage change, the capacitor can provide a large enough current to meet the requirements of the load transient current. This ensures that the variation of the load chip voltage is within the allowable range. Here, it is equivalent to that the capacitor stores a part of the electric energy in advance and releases it when the load needs it, that is, the capacitor is an energy storage element. The existence of the energy storage capacitor enables the energy consumed by the load to be quickly replenished, thus ensuring that the voltage across the load does not change too much. At this time, the capacitor plays the role of a local power supply.
Understanding capacitors from the perspective of energy storage can easily lead to an illusion that the larger the capacitor, the better. And it is easy to mislead people into thinking that the energy storage effect occurs in the low frequency band, and it is not easy to expand to the high frequency. In fact, the function of any capacitor can be explained in terms of energy storage. The following example.
Figure 2. Capacitor energy storage function extends to high frequency
As shown in the figure above, assuming that at low frequency, such as tens of kHz, since the inductive reactance generated by the low frequency signal on the inductor can be ignored, the ESL of the capacitor at the low frequency can be approximately equal to 0. When the load needs a large current instantaneously (tens of kHz), the capacitor can supply power to the load through the ESR, and the real-time power supply is very high. The eSR only consumes a part of the power, but does not affect the real-time power supply. Because the frequency is relatively low, the discharge time is relatively long (the reciprocal of the frequency), so the capacity of the capacitor needs to be larger, which can be discharged for a long time. Therefore, low-frequency energy storage is easy to understand.
With the same large capacitance, assuming that the frequency of the load mutation is high (tens of Mhz or higher), then when the load changes accordingly (tens of Mhz or higher), the inductive reactance formed on the ESL cannot be ignored. This inductive reactance A back electromotive force will be generated to prevent the capacitor from supplying power to the load, so the transient performance of the current actually obtained on the load is relatively poor, that is, the current of the capacitor cannot supply the instantaneous current sudden change, although the capacitor capacity is large, but due to the large ESL , the large-capacity energy storage cannot play a role at this time. In fact, the higher the frequency, the shorter the time for the capacitor to supply power to the load (the inverse of the frequency), and the capacitor does not need as much energy storage. For high frequency, the key factor is ESL. To reduce the ESL of the capacitor, choose a small capacitor with a small package, and the ESL will be significantly reduced. This is why we choose a small capacitor at high frequency. In addition, the inductance introduced by the trace length will also be converted to In the ESL parameter, so the small capacitor must be close to the pin.
This understanding of energy storage can even be extended to pF capacitors. In theory, assuming that there is no ESR, ESL and the transmission impedance is 0, a large capacitor is fully capable of all frequencies. But this assumption does not exist. Therefore, a reasonable combination of large and small capacitors is required in the circuit to cope with the supply of loads at different frequencies. And the closer the capacitor is to the load, the less the effect of the transmission line's equivalent inductance and resistance.
Figure 3 Mobile phone Vbat power supply capacitor allocation diagram
For example, in the mobile phone design, 47uf capacitors are hung on several branches of the vbat power supply branch. As shown in the figure above, there are 47uf capacitors near the connector, near the PMU, and near the PA. It is believed that only the 47uf next to the PA has a good effect on the PA. The effect, the one next to the connector and the one next to the PMU has no effect on the PA. In fact, this is not the case. When the PA needs an instantaneous current, the three tantalum capacitors will supply power to the PA. The power supply process depends entirely on the instantaneous voltage difference. The instantaneous pressure difference of the PA is the largest, whichever power supply is more active. Capacitors away from the PA need to consider the impedance and inductive reactance of the transmission line. For low frequencies, this parasitic inductance can be ignored. For 217HZ, the current required by the PA is far from enough for the three capacitors to add up, so when the GSM is high power, the PA draws current from all three capacitors.
For low frequencies, the role of parasitic inductance can be ignored. The distance between these large capacitors and the chip is only reflected in the wiring resistance. Generally, the voltage drop of the wiring resistance of the power supply line is within 100 milliohms, which has very little effect on the charging and discharging of the capacitor. Therefore, it can be considered that Large capacitors on the motherboard do not need to be very close to the chip.
Understanding power supply decoupling from the perspective of energy storage is very intuitive and easy to understand, but it is not very helpful for circuit design. Because it is not easy to consider from a quantitative perspective, it is suitable for qualitative analysis. Understanding capacitive decoupling from the perspective of impedance allows us to have rules to follow when designing circuits. In fact, the concept of impedance is used when determining the decoupling capacitance of a power distribution system.
2. Understand the principle of decoupling from the perspective of impedance.
Remove the load chip in Figure 1, as shown in Figure 2. Looking to the left from the two points AB, the regulated power supply and the capacitive decoupling system together can be regarded as a composite power supply system. The characteristics of this power supply system are: no matter how the load transient current changes between the two points AB, the voltage between the two points AB can be guaranteed to remain stable, that is, the voltage change between the two points AB is very small.
Figure 4 Power section
We can use an equivalent power model to represent the above composite power system, as shown in Figure 3, the series model of constant voltage source and internal resistance.
The following equation can be written for this circuit:
Assuming that the power supply is an ideal voltage source, that is, Z=0, and assuming that the impedance of the transmission path is also 0, then no matter how the load changes and how fast the change is, the voltage source can respond and ensure that A and B are both The point voltage is always constant. But in fact, the internal resistance of the power supply is not zero, and the transmission line is not ideal, and these influencing factors are complex numbers and are related to frequency, so the PDN impedance of the power supply appears.
Our final design goal is to keep the voltage variation range between the two points AB very small no matter how the load transient current changes between the two points AB. According to Equation 2, this requirement is equivalent to the impedance Z of the power system being low enough. In Figure 4, we achieve this requirement through decoupling capacitors, so from an equivalent point of view, it can be said that decoupling capacitors reduce the impedance of the power system. On the other hand, from the point of view of circuit principle, the same conclusion can be obtained. Capacitors have low impedance characteristics for AC signals, so adding capacitors does actually reduce the AC impedance of the power system.
Understanding capacitive decoupling from the perspective of impedance can bring great convenience to the design of power distribution systems. In fact, the most fundamental principle of power distribution system design is to minimize impedance. The most effective design methods are guided by this principle.
In order to understand the concept of the output impedance (internal resistance) of the power supply, let us recall the definition of the internal resistance of the power supply: disconnect the load, looking in from the load end, the constant voltage source is short-circuited, and the cross-current source is open-circuited. As shown in Figure 6.
Figure 6 Equivalent diagram of power supply internal resistance
It can be seen from Figure 6(b) that after paralleling the capacitors, the internal resistance of the power supply seen from the load side has a new change, that is, Z'=Z//Z1, where Z1 is the capacitive reactance of the capacitor. Visible new internal resistance Z'
The capacitive reactance in Figure 6 cannot be simply calculated using jwC, because the capacitance is not an ideal model, it contains ESR, ESL, and these require an actual measured model. Figure 7 shows the |Z| curve of a 47uF tantalum capacitor. It reflects the impedance value of this capacitor at different frequencies (without considering the phase information). As can be seen from the figure, the lowest point of the capacitor impedance is 8 milliohms at the frequency of 700K.
Figure 7 Z curve of 47uF tantalum capacitor
This graph is the measured value and contains all the information about the capacitor (except the phase).
For example: it contains the capacitance information of the capacitor. Generally, the larger the capacitance, the lower the resonance point. To reach the resonance point of 700k, only the capacitance near this capacitance value can be achieved. A 0.1uf capacitor cannot reach this frequency anyway. It contains ESL information. Assuming ESL=0, the curve is a straight line with a slope. It also contains ESR information, such as 8 milliohms at the resonance point is its ESR value. Therefore, if we use impedance characteristics to describe capacitors, we must not use the concept of current storage. For example, there are some differences between using 10uF capacitors on PMU and using 4.7uf capacitors from the impedance curve, but we can accept it. Do not use current storage as an excuse to say that 10uF has more energy storage than 4.7uF, so the effect is good. The two research methods are to analyze the same problem from different angles, and they will be confused when intertwined. It is recommended to use impedance method analysis, which can do quantitative analysis.
For example, if we design an anti-surge circuit, the waveform of a general surge signal is shown in Figure 8.
Figure 8 Surge waveform of 0.5us-100kHz
Assuming that we want to eliminate the surge waveform shown in Figure 8, we need to add capacitors, but how much capacitors are added, if the analysis from the perspective of capacitor charging and discharging is very complicated, it is not easy to explain in one or two pages. But if we analyze from the impedance point of view, we only need a simple requirement, that is, add a capacitor, so that the harmonic shown in Figure 8 is short-circuited to GND, and the surge is eliminated. How to achieve this requirement? A capacitor must be selected so that the impedance of the capacitor to the frequency of the surge signal is the lowest. So the idea is clear, follow two steps:
1 Determine the frequency of the surge signal. As can be seen from Figure 8, the surge signal is similar to a sine wave, and the fundamental frequency is about 100khz. There are some high-order harmonics only at the initial moment. This high-order harmonic can be estimated, which is about a few Mhz levels.
2 Find two capacitors, one with resonance point at 100kHz to eliminate the fundamental signal in the surge signal. Find another capacitor with a resonance point of several Mhz to eliminate higher harmonics in the surge signal. If the high-order harmonics of the surge signal are not accurately estimated, a few more capacitors in other possible frequency bands can be added.
In actual operation, it is found that even the capacitance of 470uf has a resonance point of 200k, and the capacitance of the resonance point of 100khz is estimated to be larger. It is impossible for a mobile phone to place such a large capacitor, so we can only look at the impedance of 47uF (the largest capacitor that can be placed on a mobile phone) to 100kz. 470uF has an impedance of 3 milliohms at 200khz and 5 milliohms at 100khz. The 47uf has an impedance of 40 milliohms at 100khz. It is acceptable, if a 47uF capacitor is connected in parallel, the impedance will be halved at 100khz to 20 milliohms. Personally think that for surge signals, short-circuit resistance within 0.1 ohms can meet the requirements. According to this requirement, the capacitor can also be made smaller. The principle of capacitance is the same for electrostatic protection. Before protection, you must know the spectrum of static electricity.
For the capacitor layout shown in Figure 3, in fact, all three 47uF capacitors have a protective effect against surges, but these three capacitors are not in a direct parallel relationship. The actual model of these three capacitors for electrostatic protection is analyzed in detail below.
If the surge is entering from the battery connector, the impedance at the battery connector should be analyzed. As shown in Figure 9, the layout capacitance of Figure 3 is equivalent. After the equivalent, it can be seen that the layout positions of Zc1 and Zc2 are far away, and the capacitance test model cannot be used for surge protection. With the addition of LX, the capacitance of | The Z| curve will be shifted to the left, and with the addition of RX, the |Z| curve will be shifted upward. The size of the movement depends on the magnitude of LX and Rx, which make the capacitor's protection against surges worse. Specifically, it can be realized through PCB simulation. Through simulation, the impedance of 100khz at the entrance of the connector can be obtained, so as to know the effect of surge protection. Generally speaking, in the low frequency band of 100k, the influence of Lx can be ignored.
Figure 9 Schematic diagram of three 47uF capacitors in different positions for protection against surge
As can be seen from the above figure, the capacitance of the layout source actually plays a role in surge protection, but the effect is not as good as the layout at the connector, and the difference needs to be simulated to quantify.
Extending to the example in our work, what is the function of placing a 22uF capacitor next to the PA? In 2012, it was interpreted as surge protection, and it was also required to be placed near the pin. I don't quite understand this, where does the surge come from? If it comes from the connector, it should be placed near the connector first. From the perspective of reducing voltage sag, let's take a look at this model
From the perspective of energy storage, it is better to understand that when the PA needs current, the voltage will drop. If the capacitor supplies part of the current to the PA, the voltage will drop slightly, but how much it can be reduced cannot be quantified. From the perspective of impedance, a 217Hz square wave appears on the power supply, and we need to add a capacitor to short-circuit this square wave (which can be considered as an interference wave) to GND. The spectrum of the square wave includes 217Hz and its multiples. The part with the largest amplitude is the fundamental wave. We must first find a way to filter the fundamental wave. The way to filter it is to find a capacitor whose resonance point is at 217Hz. For a low frequency, we can think that ESL has no effect on it, then the capacitive reactance can be calculated using the ideal model 1/jwc. Assuming that the ideal impedance is 0.1 ohms, then through calculation, the required capacitance is 7338uF. Even with a nominal 6800, 1000uf capacitor filter, the obvious effect can be seen. So how capable can our 22uF capacitor be! Only some octave spectrum can be filtered out.
It can be seen from this example that what can be explained from the perspective of energy storage can also be explained by using impedance, and quantitative analysis can be easily done by using impedance analysis methods.
Power supply decoupling involves many questions: How much total capacitance is required to meet the requirements? How to determine this value? Which capacitor values ​​to choose? How many capacitors are there? What kind of capacitor to choose? How are the capacitors mounted on the board? What are the requirements for capacitor placement distance? They are introduced separately below.
Target Impedance is defined as:
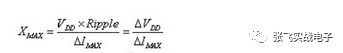
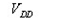
There are two things to note about the target impedance:
1. The target impedance is the transient impedance of the power system, which is an impedance characteristic exhibited by the rapidly changing current.
2. The target impedance is related to a certain width of the frequency band. The source impedance cannot exceed this value over the entire frequency range of interest. Impedance is the result of the combined action of resistance, inductance and capacitance, so it must be frequency dependent. What is the overall frequency range of interest? This is related to the transient current requirements of the load. As the name implies, transient current is the current that a power supply must supply for a very short period of time. If this current is regarded as a signal, it is equivalent to a step signal with a wide spectrum, and this spectrum range is the frequency range we are interested in.
How much capacity is needed:
There are two ways to determine the required capacitance. The first method uses the load driven by the power supply to calculate the capacitance. This method does not take into account the influence of ESL and ESR, so it is very imprecise, but it is good for understanding the choice of capacitance. The second method is to use the target impedance (TargetImpedance) to calculate the total capacitance, which is a common method in the industry and has been widely verified. You can use this method to calculate first, and then perform local fine-tuning, which can achieve good results. How to perform local fine-tuning is a more advanced topic. The two methods are described below.
Method 1: Calculate the capacitance using the load driven by the power supply
Let the load (capacitive) be 30pF, to drive from 0V to 3.3V in 2ns, the transient current is:
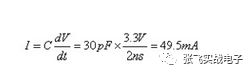
If a total of 36 such loads need to be driven, the transient current is: 36*49.5mA=1.782A. Assuming the allowable voltage fluctuation is: 3.3*2.5%=82.5mV, the required capacitance is
C=I*dt/dv=1.782A*2ns/0.0825V=43.2nF
Note: The added capacitor is actually an energy storage element for suppressing voltage ripple. The capacitor must provide a current of 1.782A to the load within 2ns, and the voltage drop cannot exceed 82.5 mV, so the capacitance value should be calculated based on 82.5 mV. Remember: capacitor discharge to supply current to the load, its own voltage will also drop, but the voltage drop cannot exceed 82.5mV (tolerable voltage ripple). This kind of calculation has no practical significance. The reason why I put it here is to let everyone have a deeper understanding of the decoupling principle.
Method 2: Calculate capacitance using target impedance
In order to clearly illustrate the calculation method of capacitance, we use an example. The decoupling power supply is 1.2V, the allowable voltage fluctuation is 2.5%, and the maximum transient current is 600mA.
Step 1: Calculate the target impedance

Step 2: Determine the frequency response range of the regulated power supply.
It is related to the specific power supply chip used, usually between DC and several hundred kHz. Here it is set to DC to 100kHz. Below 100kHz, the power chip can respond well to the transient current, and when it is higher than 100kHz, it shows a very high impedance. If there is no external capacitor, the power supply fluctuation will exceed the allowable 2.5%. How much capacitance should be added to meet the requirement of less than 2.5% voltage fluctuation above 100kHz?
Step 3: Calculate the bulk capacitance
When the frequency is below the self-resonance point of the capacitor, the impedance of the capacitor can be approximately expressed as:

The higher the frequency f, the lower the impedance, and the lower the frequency, the higher the impedance. In the frequency range of interest, the maximum impedance of the capacitor cannot exceed the target impedance, so 100kHz is used for the calculation (the lowest frequency in the frequency range where the capacitor functions, corresponding to the highest impedance of the capacitor).
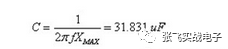
Step 4: Calculate the Highest Effective Frequency of the Bulk Capacitor
When the frequency is above the self-resonance point of the capacitor, the impedance of the capacitor can be approximately expressed as:
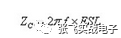
The higher the frequency f, the higher the impedance, but the impedance cannot exceed the target impedance. Assuming ESL is 5nH, the highest valid frequency is:

Such a large capacitor allows us to keep the source impedance below the target impedance between 100kHz and 1.6MHz. At frequencies above 1.6MHz, additional capacitors are required to control the power system impedance.
Step 5: Calculate the capacitance required for frequencies above 1.6MHz
If the power supply system is expected to meet the voltage fluctuation requirements below 500MHz, the parasitic inductance of the capacitor must be controlled. must meet
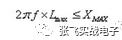
So have:

Assuming the use of 0402 package ceramic capacitors, the parasitic inductance is about 0.4nH, plus after mounting on the circuit board
The parasitic inductance of the via (calculated later in this article) is assumed to be 0.6nH, resulting in a total parasitic inductance of 1nH. In order to meet the requirement that the total inductance is not greater than 0.16 nH, the number of capacitors we need in parallel is: 1/0.016=62.5, so 63 0402 capacitors are required.
In order for the impedance to be less than the target impedance at 1.6MHz, the required capacitance is:
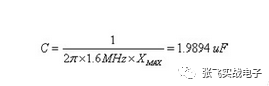
So the capacitance of each capacitor is 1.9894/63=0.0316 uF.
To sum up, for this system, we choose 1 large capacitor of 31.831 uF and 63 small capacitors of 0.0316 uF to meet the requirements.
Liquid Crystal Display For Instrument
Liquid Crystal Display For Instrument,Large Industrial Precision Lcd Display,Small Industrial Body Thin Lcd Display,Precise Liquid Crystal Display
Dongguan Yijia Optoelectronics Co., Ltd. , https://www.everbestlcdlcms.com