Wavelet transform (WT) is a new transform analysis method. It inherits and develops the idea of ​​localization of short-time Fourier transform. At the same time, it overcomes the shortcomings of window size and frequency variation, and can provide a change with frequency. The “Time-Frequency†window is an ideal tool for signal time-frequency analysis and processing.
Its main feature is that it can fully highlight some aspects of the problem through transformation, can localize the analysis of time (space) frequency, and gradually multi-scale the signal (function) through the telescopic translation operation, and finally reach the high frequency. Time subdivision, frequency subdivision at low frequency, can automatically adapt to the requirements of time-frequency signal analysis, so that it can focus on any detail of the signal, solve the difficult problem of Fourier transform, and become a major breakthrough in scientific methods since the Fourier transform.
Multi-scale concept1. The so-called multi-scale means that in the RBF network, the nodes that use the variance of different kernel functions have different roles. The nodes with large kernel function variances play a larger role, so they are more inclined to represent the training set. Overall information.
2. Multi-scale means that the GEM forms a GEM mesoscale mode, a GEM regional mode, a GEM global mode, and a GEM low-resolution mode according to different resolutions under the same basic architecture.
3. When aj0 "1" is called multi-scale, the discrete wavelet function ψj, k(t) is obtained from the compatibility condition as ψj, k(t)=a-j20ψt-kaj0b0aj0=a-j20ψ(a- J0t-kb0) (6) and the discretized wavelet transform coefficient can be expressed as Cj.
The wavelet transform has two factors: one is the time shift factor and the other is the scale factor. The scale factor a, a "1" indicates stretching, and a "1 indicates contraction. Generally go to the root number a, the purpose is to ensure energy conservation. The resulting wavelet signal is a detail signal, and the wavelet transform is known as a microscope.

First, from wavelet analysis to multi-scale geometric analysis
One of the key reasons for the great success of wavelet analysis in multidisciplinary fields is that it can represent one-dimensional piecewise smooth or bounded variograms more sparsely than Fourier analysis. Unfortunately, the excellent characteristics of wavelet analysis in one dimension cannot be simply extended to two or higher dimensions. This is because the one-dimensional wavelet-separated Separable wavelet has only a finite direction and cannot "optimally" represent a high-dimensional function with line or surface singularity, but in fact the function with line or surface singularity is high. It is very common in dimensional space. For example, the smooth boundary of natural objects makes the discontinuity of natural images often manifest as singularity on smooth curves, not just singularity. In other words, in high-dimensional cases, wavelet analysis does not make full use of the unique geometric features of the data itself, not the optimal or "sparse" function representation; and the multi-scale geometry developed after wavelet analysis. The purpose and motivation of the development of MulTIscale Geometric Analysis (MGA) is to develop an optimal representation of a new high-dimensional function. In order to detect, represent, and process certain high-dimensional spatial data, the main features of these spaces Yes: Some important features of the data are concentrated in its low-dimensional subsets (such as curves, faces, etc.). For example, for a two-dimensional image, the main features can be characterized by edges, while in 3-D images, important features are embodied as filaments and tubes.
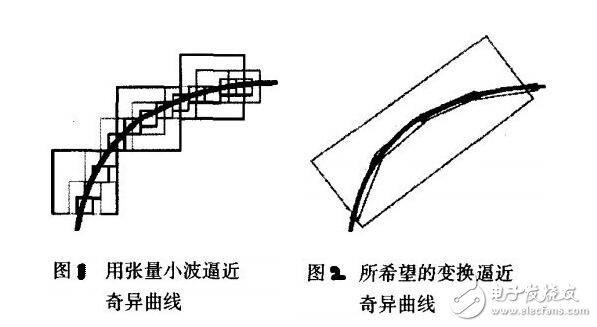
The two-dimensional wavelet base formed by the one-dimensional wavelet has a square support interval. Under different resolutions, the support interval is a square of different sizes. The process of two-dimensional wavelet approximating the singular curve is finally expressed as a process of approximating the line with "points". On the scale j, the side length of the wavelet support interval is approximately 2-j, and the number of wavelet coefficients whose amplitude exceeds 2-j is at least O(2j). When the scale becomes thinner, the number of non-zero wavelet coefficients is indexed. Form growth, a large number of non-negligible coefficients appear, and ultimately the performance can not be "sparse" to represent the original function. Therefore, we hope that when a certain transform is approaching the singular curve, in order to make full use of the geometric regularity of the original function, the support interval of the base should be expressed as "long strip" to achieve the approximating the singular curve with the least coefficient. The "long strip" support interval of the base is actually an embodiment of "direction", also known as "anisotropy". The transformation we hope for is "multiscale geometric analysis."
The multi-scale geometric analysis methods of images are divided into two types: adaptive and non-adaptive. The adaptive method generally performs edge detection and then uses edge information to optimally represent the original function. In fact, it is a combination of edge detection and image representation. Such methods are represented by Bandelet and Wdgelet; non-adaptive methods do not know the geometric features of the image itself a priori, but directly decompose the image on a fixed set of bases or frames, which is free of The dependence of the image's own structure, which is represented by Ridgelet, Curvelet, and Contourlet transforms.
Second, several multi-scale geometric analysis1, Ridgelet (Ridgelet) transformation
Ridgelet theory was proposed by Emmanuel J Candès in his doctoral thesis in 1998. This is a non-adaptive high-dimensional function representation with direction selection and recognition capabilities to more effectively represent directionality in signals. The singular features. The ridgelet transform firstly performs Radon transform on the image, that is, the singularity in the image, such as the straight line in the image, is mapped to a point in the Randon domain, and then the singularity is detected by the one-dimensional wavelet, thereby effectively solving the wavelet transform. The problem when dealing with 2D images. However, the edge lines in the natural image are mostly curved, and the Ridgelet analysis of the entire image is not very effective. In order to solve the sparse approximation problem of multi-variable functions with curve singularity, in 1999, Candes proposed a single-scale ridge wave (MonoscaleRidgelet) transformation, and gave its construction method. Another method is to block the image so that the lines in each block are approximate straight lines, and then perform a Ridgelet transform on each block. This is a multi-scale Ridgelet. The ridgelet transform has good approximation performance for multivariable functions with linear singularity, that is, for texture (line singularity) rich images, Ridgelet can obtain a more sparse representation than wavelet; but for multivariate functions with curve singularity Its approximation performance is only equivalent to wavelet transform, and it does not have the optimal nonlinear approximation error attenuation order.
2, Curvelet (Curvelet) transformation
Due to the large redundancy of multi-scale Ridgelet analysis, Candès and Donoho proposed a continuous curvelet transform based on the Ridgelet transform in 1999, namely Curvelet99 in the first generation Curvelet transform; in 2002, Strack, Candès and Donoho proposed Curvelet02 in the first generation of Curvelet transforms. The first generation Curvelet transform is essentially derived from Ridgelet theory and is a transformation based on Ridgelet transform theory, multiscale Ridgelet transform theory and bandpass filter theory. The basic scale of the single-scale ridgelet transform is fixed, but the Curvelet transform is not. It is decomposed at all possible scales. In fact, the Curvelet transform is a special filtering process and multi-scale ridgelet transform (MulTIscale Ridgelet Transform). The combination is: first sub-band decomposition of the image; then different size sub-band images of different sizes are used; finally, each block is subjected to Ridgelet analysis. Like the definition of calculus, at a sufficiently small scale, the curve can be seen as a straight line, and the curve singularity can be represented by the linear singularity, so the Curvelet transform can be called the "integration of the Ridgelet transform".
The first generation of Curvelet digital implementation is more complex, requiring a series of steps such as sub-band decomposition, smooth partitioning, normalization and Ridgelet analysis, and the decomposition of the Curvelet pyramid also brings huge data redundancy, so Candès et al. In 2002, a fast Curvelet transform algorithm that is simpler and easier to understand is proposed, namely the second generation Curvelet (FastCurvelet transform). The second generation of Curvelet is completely different in construction from the first generation of Curvelet. The first generation of Curvelet's construction idea is to approximate the curve to each straight block by a small enough block, and then use the local Ridgelet to analyze its characteristics, while the second generation of Curvelet and Ridgelet theory has nothing to do with The process does not need to use Ridgelet. The similarities between the two are only the abstract mathematical meanings of tight support and framework. In 2005, Candès and Donoho proposed two fast discrete Curvelet transform implementation methods based on the second generation Curvelet transform theory, namely: Unequally-Spaced Fast Fourier Transform (USFFT) and Wrap algorithm ( Wrapping-BasedTransform). For the Curvelet transform, the Matlab package Curvlab can be downloaded from the Internet; the Curvlab package contains Curvelet's fast discrete algorithm Matlab program and C++ program.
3, contour wave (Contourlet) transformation
In 2002, MN Do and MarTIn Vetterli proposed a "real" two-dimensional representation of images: the Contourlet transform, also known as the Pyramidal DirecTIonal Filter Bank (PDFB). The Contourlet transform is another multi-resolution, localized, directional image representation method implemented using Laplacian Decomposition (LP) and Directional Filter Bank (DFB).
The Contourlet transform inherits the anisotropic scale relationship of the Curvelet transform, so in a certain sense, it can be considered as another fast and efficient digital implementation of the Curvelet transform. The support interval of the Contourlet basis is a "long strip" structure with an aspect ratio that varies with the scale, with directionality and anisotropy. In the Contourlet coefficient, the coefficient energy representing the edge of the image is more concentrated, or the Contourlet transform has more curves. "Sparse" expression. The Contourlet transform splits the multi-scale analysis and the direction analysis. First, the image is multi-scaled by LP (Laplacian pyramid) transformation to "capture" the point singularity, and then distributed by the Directional Filter Bank (DFB). The singular points in the same direction are combined into one coefficient. The final result of the Contourlet transform is to approximate the original image with a base structure similar to the Contour segment, which is why it is called the Contourlet transform. The two-dimensional wavelet is constructed by one-dimensional wavelet tensor product, and its base lacks directionality and has no anisotropy. It can only be limited to describing the contour with a square support interval, and the squares of different sizes correspond to the multi-resolution structure of the wavelet. When the resolution becomes fine enough, the wavelet becomes a point to capture the outline.
4, band wave (Bandelet) transformation
In 2000, Ele Pennec and Stephane Mallat were in the literature "EL Pennec, S Mallat. Image compression with geometrical wavelets [A]. In Proc. Of ICIP' 2000 [C]. The Bandelet transform is proposed in Vancouver, Canada, September, 2000. 661-664. Bandelet transform is an edge-based image representation method that can adaptively track the geometric regular direction of an image. Pennec and Mallat believe that in the image processing task, if the geometric regularity of the image can be known in advance and fully utilized, the approximation performance of the image transformation method will undoubtedly be improved. Pennec and Mallat first defined a geometric vector line that can characterize the local regular direction of the image. Then, the support interval S of the image is binary-divided into S=∪iΩi. When the section is sufficiently thin, each section is divided into Ωi. It only contains at most one outline (edge) of the image.
In all local regions Ωi that do not contain contours, the changes in image gray values ​​are consistent, so the direction of the geometric vector lines is not defined in these regions. For a local area containing a contour, the direction of the geometric regularity is the tangent direction of the outline. According to the local geometric regular direction, under the global optimal constraint, the vector line of the vector field τ(x1, x2) in the region Ωi is calculated, and the interval wavelet defined in the Ωi is bandedletized along the vector line to generate the Bandelet. Base to be able to take full advantage of the local geometric regularity of the image itself. The process of Bandeletization is actually a process of wavelet transform along a vector line, which is called a warped wavelet transform. Thus, the set of Bandelets on all of the split regions Ωi constitutes a set of standard orthogonal bases on L2(S).
The Bandelet transform adaptively constructs a local bending wavelet transform according to the image edge effect, transforming the curve singularity in the local region into a linear singularity in the vertical or horizontal direction, and then using ordinary two-dimensional tensor wavelet processing, and two-dimensional The tensor wavelet base can effectively deal with the singularity in the horizontal and vertical directions. Thus, the key to the problem comes down to the analysis of the image itself, namely how to extract the prior information of the image itself, how to split the image, how to "track" the singular direction in the local area, and so on. However, in natural images, the mutation of the gray value does not always correspond to the edge of the object. On the one hand, the diffraction effect makes the edge of the object in the image may not obviously show the mutation of the gray scale; on the other hand, many times The gray value of the image changes drastically, not from the edge of the object but due to changes in the texture.
A common problem that all edge-based adaptive methods need to solve is how to determine whether the region of the image where the gray value changes drastically corresponds to the edge of the object or the texture. This is actually a very difficult problem. Most of the edge-based adaptive algorithms in practical applications, when the image appears more complex geometric features, such as Lena image, in the sense of approximation error, the performance can not exceed the separable orthogonal wavelet analysis. In low bit rate encoding of an image, the overhead used to represent the location of the non-zero coefficients is much greater than the overhead used to represent non-zero coefficient values. Compared with wavelet, Bandelet has two advantages: (1) make full use of geometric regularity, the energy of the high frequency sub-band is more concentrated, and the non-zero coefficient is relatively reduced under the same quantization step; (2) benefit from the quadtree structure And geometric flow information, Bandelet coefficients can be rearranged, and the coefficient scanning method is more flexible when encoding. Explain the potential advantages of Bandelet transform in image compression.
The central idea of ​​constructing a Bandelet transform is to define the geometric features in the image as vector fields rather than as ordinary edge sets. The vector field represents the local regular direction of the gray value change of the image space structure. The Bandelet base is not predetermined, but adaptively selects the composition of the specific base by optimizing the final application results. Pennec and Mallat give the optimal basis fast finding algorithm for Bandelet transform. The preliminary experimental results show that Bandelet has certain advantages and potentials in denoising and compression compared with ordinary wavelet transform.
5, Wedgelet transform
In multi-scale geometric analysis tools, Wedgelet transforms have good "line" and "face" characteristics.
Wedgelet is a direction information detection model proposed by Professor David L. Donoho when studying the problem of recovering original images from noisy data. Wedgelet transform is a concise representation of image outlines. Using a multi-scale Wedgelet to segment the image linearly, the block size can be automatically determined based on the image content, and the features of the lines and faces in the image are better captured. Overcome the shortcomings of the sliding window method.
The multiscale Wedgelet transform consists of two parts: multiscale Wedgelet decomposition and multiscale Wedgelet representation. Multi-scale Wedgelet decomposition divides the image into image blocks of different scales and projects each image block into Wedgelets of each allowable orientation; the multi-scale Wedgelet representation selects the best partition of the image according to the decomposition result, and for each image block The optimal Wedgelet representation is selected to complete the region segmentation of the image.
What is Wedgelet? To put it bluntly, it is to draw a line segment in a dyadic square and divide it into two wedges, each of which is represented by a unique gray value. The position of the line, two gray values, approximates the nature of this sub-block.
6, small line (Beamlet) transformation
The BeamletsTransform was first proposed by Professor David L. Donoho of Stanford University in 1999 and has been initially applied. Beamlets Analysis, introduced by small-line transformation, is also a multi-scale analysis, but it is different from the multi-scale concept of wavelet analysis. It can be understood as an extension of the multi-scale concept of wavelet analysis. The small line segment of scale and position is the basic unit to establish the small line library, the small line segment integral in the image and the library generates small line transform coefficients, the transform coefficients are organized in a small line pyramid manner, and the small line transform is extracted from the pyramid by the form of the graph. Coefficients to achieve multi-scale analysis. This is a tool for better two-dimensional or higher singularity analysis.
According to the small line theory and its research results, it has unparalleled advantages for processing images with strong noise background. However, the preparatory work of the small-line transformation, such as the small-line dictionary and the small-line pyramid scan, is too large and is not conducive to research. If you can simplify this part, or make a fixed module reference, I believe that small line analysis can quickly expand its application area. In general, the research on small-line analysis is still in its infancy, and there are not many relevant research results. The field of applied research needs to be further expanded.
In the Beamlet analysis, the line segment is similar to the position of the point in wavelet analysis. Beamlet can provide local scale, position and direction representation of line segments based on binary structure. The precise positioning of lines is easy to implement and the algorithm implementation is not complicated. Therefore, the line feature extraction based on Beamlet is worth studying.
The Beamlet base is a multi-scale directional set of line segments with a binary feature. The binary feature reflects that the constant point coordinates of the line segment are binary, and the scale is also binary.
Donoho proposed continuous Beamlet transform and its application in multi-scale analysis. In order to reduce the computational complexity and be more suitable for computer processing, Xiaoming Huo proposed a discrete Beamlet transform.
According to the Beamlet-based framework, each Beamlet divides each binary square into two parts, each of which is called a Wedgelet. These two parts are complementary Wedgelets, so each Beamlet corresponds to two complementary Wedgelets. Making the Beamlet base correspond to the Wedgelet The Wedgelet transform has multi-scale characteristics; it can also be seen that the Wedgelet base is a flaky base, which is different from the linear basis of the Beamlet.
CSRME safety controller is developed for standard GB27607. By monitoring machine tool safety related equipment, the security of machine control system can meet the requirements of GB27607, and its security meets the requirements of ISO13849-1 (PLe) and IEC61508 (SIL3).
With rich interfaces, CSRME has limited programmable function. It can simultaneously replace many different types of safety control modules or safety PLCs, thus greatly simplifying the safety design of machine control systems and reducing cost.
Safety Controller,Modular Safety Controller,Safety Controller,Electrical Safety Controller,Programmable Logic Controller,Banner Safety Controller
Jining KeLi Photoelectronic Industrial Co.,Ltd , https://www.sdkelien.com